МОДУЛЬНАЯ ПРОГРАММА ЛЕКЦИОННОГО КУРСА, СЕМИНАРОВ И САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Методическое пособие, предназначенное для студентов III курса ФЕН специальности «Химия», содержит программу курса лекций в 5-м семестре, структуру курса и правила ИКИ. Кроме того, приведен набор задач для самостоятельной работы студентов (домашних заданий) и даны примеры вариантов промежуточных и экзаменационных контрольных работ за прошлые годы.
Составитель д-р хим. наук, доц. А. А. Хасин
© Новосибирский государственный университет, 2009
Для просмотра web-документов, содержащих формулы, представленные в MathML, и подготовленных указанным выше способом, необходимо наличие на вашем компьютереI. Основные понятия химической термодинамики
II. Химическое равновесие в гомогенных системах.
III. Химическое равновесие в гетерогенных системах
IV. Химическое равновесие в системах, содержащих растворы электролитов
V. Термодинамика дисперсных систем и поверхностных явлений
VI. Использование статистических методов для описания химического равновесия в идеальных системах
Основная литература:
Бажин Н. Б., Иванченко В. А., Пармон В. Н. Термодинамика для химиков. 2-е изд., М.: Колосс, 2004.
Пармон В. Н. Лекции по химической термодинамике. Новосибирск: НГУ, 2004
Музыкантов В. С., Бажин Н. М., Пармон В. Н., Булгаков Н. Н., Иванченко В. А. Задачи по химической термодинамике. М.: Химия, 2001.
Задачи по химической термодинамике (под ред. В. Н. Пармона), Новосибирск: НГУ, 2003.
Задачи по химической термодинамике (под ред. А. А. Хасина), Новосибирск: НГУ, 2009.
Бажин Н. Б., Иванченко В. А., Пармон В. Н. Термодинамика для химиков. М.: Химия, 2000.
Бажин Н. Б., Иванченко В. А., Пармон В. Н. Термодинамика для химиков. Новосибирск: НГУ, 1999. Ч. 1-2.
Дополнительная литература:
Бажин Н. Б. Краткий курс химической термодинамики. Новосибирск: НГУ, 1991. Ч. 1-2.
Голиков Г. А. Руководство по физической химии. М.: Высш. шк., 1988.
Даниэльс Ф., Олберти Р. Физическая химия. М.: Мир, 1978.
Еремин Е. Н. Основы химической термодинамики. М.: Высш. шк., 1978.
Карапетьянц М. Х. Химическая термодинамика. М.: Химия, 1975.
Киттель Ч. Статистическая термодинамика. М.: Наука, 1977.
Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. М.: Высш. шк., 1990.
Кубо Р. Термодинамика. М.: Мир, 1970.
Курс физической химии / Под ред. Я. И. Герасимова. М.: Химия, 1973.
Мюнстер Ф. Химическая термодинамика. М.: Мир, 1971.
Пармон В. Н., Иванченко В. А. Введение в курс физической химии для специализации “геохимия”. Новосибирск: НГУ, 1996.
Полторак О. М. Термодинамика в физической химии. М.: Высш. шк., 1991.
Пригожин И., Дефей Р. Химическая термодинамика. Новосибирск: Наука, 1966.
Смирнова Н. А. Методы статической термодинамики в физической химии. М.: Высш. шк., 1982.
Стромберг А. Г., Семченко Д. П. Физическая химия. М.: Высш. шк., 1999.
Шляпинтох В. Я., Замараев К. И., Пурмаль А. П. Химическая термодинамика. М.: МФТИ, 1975.
Курс изучается в течение одного семестра (осенний семестр 3-го курса). Ниже в таблице приведен тематический план.
Тематический план курса (распределение часов)
|
|
||||||
|
Наименование разделов и тем |
|
|
|
|
|
|
|
I. Основные понятия химической термодинамики |
|
|
|
|
|
|
|
II. Химическое равновесие в гомогенных системах |
|
|
|
|
|
|
|
|
||||||
|
III. Химическое равновесие в гетерогенных системах |
|
|
|
|
|
|
|
|
||||||
|
IV Химическое равновесие в системах, содержащих растворы электролитов. |
|
|
|
|
|
|
|
V.Термодинамика дисперсных систем и поверхностных явлений. |
|
|
|
|
|
|
|
VI.Использование статистических методов для описания хим. равновесия в идеальных системах |
|
|
|
|
|
|
|
|
||||||
|
Итого по курсу |
|
|
|
|
||
По окончании курса, в зимнюю сессию, студенты аттестуются на основании результата письменного экзамена. Параллельно действует ] система “индивидуального кумулятивного индекса” (ИКИ), позволяющая получить оценку без экзамена (автоматически). Все контрольные точки (коллоквиумы, контрольные работы) являются обязательными. Форму проведения коллоквиума определяет преподаватель, ведущий семинарские занятия. Результаты прохождения контрольных точек в течение семестра передаются в деканат.
Итоговую оценку за семестр студент получает исходя из суммы баллов, набранных в результате работы в семестре, и баллов, полученных на письменном экзамене. До экзамена можно набрать максимум 1700 баллов. За экзаменационную работу можно получить максимум 400 баллов. Таким образом, максимально возможная сумма составляет 2100 баллов.
Для получения оценки, не сдавая экзамен (“автомат”), студенту необходимо набрать до начала сессии не менее 1500 баллов для оценки “отлично” или не менее 1200 баллов для оценки “хорошо”.
Для получения итоговой оценки за семестр необходимо набрать в сумме за работу в семестре и на экзамене не менее 1000 баллов (оценка “удовлетворительно”), 1200 баллов (оценка “хорошо”) или 1500 баллов (оценка “отлично”) и одновременно написать экзаменационную работу на не менее, чем 200 баллов (оценка “удовлетворительно”), 280 баллов (оценка “хорошо”) или 360 баллов (оценка “отлично”). В случае, если студент имел право получить автоматически оценку “хорошо” по результатам работы в семестре и неудачно написал экзаменационную работу, он сохраняет право на получение оценки “хорошо”.
Переэкзаменовка проводится в форме письменного экзамена. Правила ИКИ на переэкзаменовке не действуют и баллы не суммируются. К переэкзаменовке с оценки “удовлетворительно” и выше студенты допускаются только с разрешения деканата.
Оценки в баллах для системы индивидуального кумулятивного индекса (ИКИ)
|
Выполнение домашних заданий: |
50 (I), | 50 (II), | 50 (III) |
|
Коллоквиумы: |
100 (I), | 100 (II), | 50 (III) |
|
Контрольные работы: |
400 (I), | 500 (II), | 400 (III) |
|
Экзаменационная работа |
400 |
Ниже приведены два варианта Домашних заданий. Вариант, выполняемый студентами, определяет преподаватель, ведущий семинары. Номера задач приведены по задачнику Музыкантов В. С. Бажин Н. М., Пармон В. Н., Булгаков Н. Н., Иванченко В. А. Задачи по химической термодинамике. М.: Химия, 2001.
Вариант 1
Задание 1
1–7, 1–15, 1–16 (a,б), 1–26, 1–30, 1–31, 1–43, 1–44, 2–3, 2–5, 2–12, 2–39, 3–8, 3–17, 4–4, 4–22, 4–57, 4–78, 5–5, 5–7, 6–24.
Для диссоциации N2O4 с образованием NO2 при 298 К КР = 0,141. Рассчитать равновесный
состав в системе при общем давлении 1 бар: а) при наличии только N2O4 в начальном состоянии; б) добавлении в систему
0,6 бар аргона (система расширяется по мере добавления Ar при постоянном общем давлении 1 бар); в) общем давлении 0,1 бар при наличии только
N2O4 в начальном состоянии.
Задание 2
8–2, 8–11, 8–13, 9–3, 9–6, 9–13, 9–17, 9–20, 9–25, 9–27, 10–4, 10–11, 10–20, 10–27, 11–2, 11–10, 11–17, 11–22, 11–49, 11–51.
Превращение кристаллической модификации углекислого кальция “арагонит” в модификацию “кальцит” при 25 °С сопровождается уменьшением
изобарно–изотермического потенциала на 190 кал/моль. При каком давлении при этой же температуре обе формы CaCO3
могут сосуществовать? Известно, что плотность арагонита 2,93, а кальцита – 2,71 г/см3.
Задание 3
7–41, 7–54, 7–56 (O2, CO2, NH3, C2H4, C3H8,
Alкр), 7–58, 12–5, 12–10, 12–18, 12–24, 12–28, 12–31, 13–4, 13–9, 13–12, 13–24, 14–7, 14–9, 15–9.
Рассчитать предельные значения СР (низкие, промежуточные и очень высокие температуры) для Н2,
C2H2, C2H4, C2H6.
Основное состояние атома кислорода расщепляется на три мультиплета с энергиями 0, 158, 227 см–1. Найти вклад в
СР атома кислорода электронной составляющей при Т = 1500 К.
Вариант 2.
Задание 1
1–3, 1–6, 1–17, 1–19, 1–23, 1–24, 1–43, 2–1, 2–2, 2–7, 2–29, 2–40, 3–2, 3–5, 3–6, 3–14, 4–5, 4–11, 4–15, 4–37, 5–4, 5–5, 6–24, 6–26
Задание 2
8–6, 8–10, 8–14, 9–4, 9–7, 9–13, 9–19, 9–20, 9–27, 9–29, 10–5, 10–13, 10–14, 10–18, 10–27, 11–3, 11–7, 11–11, 11–24, 11–30, 11–61
Задание 3
12–9, 12–12, 12–16, 12–23, 12–26, 12–29,13–5, 13–14, 13–17, 13–24, 13–25,14–6, 14–7, 14–9,15–9, 15–12,7–36, 7–37, 7–39, 7–47, 7–60.
Контрольная работа 1 (2008/2009 уч. г.)
Задача 1 (80 баллов)
|
Студент–химик поет песню, вдохнув вместо воздуха He. Используя таблицу, найдите, какая нота звучит вместо ноты “до”. Известно, что скорость звука в газе определяется соотношением
V - мольный объем газа, М -молярная масса газа. Сp воздуха и He равны 29,15 и 20,78 Дж/(моль·К) соответственно. Газы считать идеальными. |
|
Задача 2 (80 баллов)
Найти абсолютную стандартную энтропию твердого аммиака при Т = 15 К, если известно, что при этой температуре cр
= 0.84 Дж/(моль·К), а в диапазоне температур 0-25 К теплоемкость описывается формулой Дебая: c
р=a Т 3.
Задача 3 (80 баллов)
Константа реакции паровой конверсии СО (СО + Н2О -> CO2 + H2)
при 673,3 K составляет 12,24, а при 652,2 K - 15,28. Оцените, при какой температуре должна подаваться в адиабатический аппарат смесь
состава 12 % СО, 5% СО2, 38 % H2, 45 % H2O, чтобы равновесное содержание СО в газе на выходе
из реактора составляло менее 2 %. При оценке можно пренебречь изменением теплоемкости смеси в ходе реакции, Δ
rcp = 0 и полагать сp реакционной смеси равной 33 Дж/(моль К).
Задача 4 (80 баллов)
Углеводород A участвует в двух реакциях, приводящих к получению изомеров В и С:
A = B и A = С.
Значения стандартных энтальпий, энтропий и потенциалов Гиббса образования указанных веществ при
1000 К приведены в таблице
|
Вещество |
Δ fH0 , кДж/моль |
Sf0, Дж/моль·К |
ΔfG 0 , кДж/моль |
|
А (Перилен) |
253,2 |
987,9 |
-734,7 |
Определите равновесный состав при 1000 К. Какой из изомеров будет преобладать при последующем повышении температуры?
Задача 5 (80 баллов)
Оцените коэффициент летучести для метанола при P =30 атм, T =500 K.
P = RT/(V–b) – a/V2, где a = 0,965 м6 Па/моль2; b = 6,7 10–5 м3/моль.
Молярный объем газа при указанных условиях составляет 1,2 л.
Задача 6 (дополнительная, 100 баллов, но при условии, что в сумме не более 400 баллов)
Раздельное окисление СО водяным паром проводят следующим образом. В сосуд, содержащий 2 моля Н2О при 1 атм, помещают
порошок металлического никеля массой 0.01 г, дожидаются окончания всех химических превращений. Затем порошок извлекают из 1–го сосуда и
помещают во второй сосуд, содержащий 1 моль СО при 1 атм, и также дожидаются окончания всех химических превращений. После чего процедуру
повторяют, т. е. порошок периодически приводят в контакт с реагентами в первом и во втором сосудах, где поддерживают постоянную температуру 600 К.
Найти состав смесей в обоих сосудах после 50 повторных циклов. Известны константы равновесия реакций при Т = 600 К:
|
H2O(газ) + Ni(α) = NiO + H2 |
KP1 (600 K) = 1,6. 10– 3 |
Контрольная работа 2 (2008/2009 уч. г.)
Задача 1 (100 баллов)
Зависимости давления насыщенного пара для твердой и жидкой муравьиной кислоты (в мм рт. ст.) от температуры выражаются уравнениями:
Задача 2 (100 баллов)
Известно, что парциальный мольный объем K2SO4 в водном растворе при 25 oC описывается уравнением
где m - моляльность исследуемого раствора. Мольный объем чистой воды при 25 oC примите равным 18,079 см3 моль–1. Определите объем раствора, приготовленного из 1 моля сульфата калия и 1000 граммов воды.
|
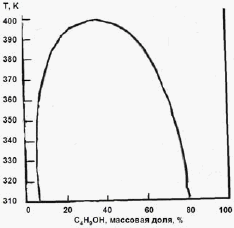
Задача 3 (100 баллов) На основании фазовой диаграммы “жидкость - пар” для системы H2O - C4H9OH оцените коэффициенты активности воды в сосуществующих фазах при 350 К. Каким будет давление пара воды над системой, содержащей 3 моля H2O и 2 моля C4H9OH? |
|
Задача 4 (100 баллов)
В индивидуальном состоянии жидкости А и В имеют одинаковые температуры кипения и энтальпии испарения, равные 123,0 oC
и 16,62 кДж/моль соответственно. Жидкости не смешиваются при любом их соотношении. Приготовлена двухфазная смесь с использованием
1 моля жидкости А и 4 молей жидкости В. При какой температуре закипит смесь? Каким будет состав дистиллята?
Задача 5 (100 баллов)
Энтальпия плавления нафталина при нормальной температуре его плавления (80,0 oC) равна 19,29 кДж/моль. При температуре
20 оС проводится эксперимент по приготовлению насыщенного раствора нафталина в гексане. Будет ли получен насыщенный раствор
при добавлении 0,48 моля нафталина к 0,72 моля гексана? Какова вариантность системы, включающей насыщенный раствор и равновесную с ним газовую
фазу?
Задача 6 (дополнительная, 100 баллов, но при условии, что в сумме не более 500 баллов)
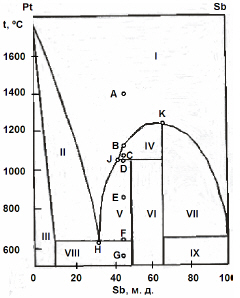
На рисунке приведена фазовая диаграмма плавкости для бинарной системы “Pt-Sb”. Назовите равновесные фазы и укажите их число в областях I-IX.
Опишите, что будет происходить с системой при охлаждении расплава с содержанием Sb 45 % от 1400 ºС (точка А) до 550 ºС (точка G).
Каково состояние системы в точках B, C, D, E, F? Как называются точки Н, J, K?
Контрольная работа 3 (2007/2008 уч. г.)
Задача 1 (80 баллов)
Растворимость Ag2CrO4 в воде при 25 oC равна 8.0 10–5 М, а в 0,04 М растворе
NaNO3 - 8,84 10–5 M. Рассчитайте среднеионный коэффициент активности Ag2CrO4 в 0,04 М
растворе NaNO3.
Задача 2 (80 баллов)
Ферментативная цепь дыхания заканчивается цитохромоксидазой, переносящей электроны на активированный кислород. Суммарная реакция
может быть представлена в виде:
2 [cyt с]- + ½
O2 + 2 H+ = 2[cyt с] + H2O,
E0’ (25oC, pH = 7) = + 0,562 В отн. НВЭ
Чему равен стандартный потенциал Гиббса реакции? В какую сторону пойдет реакция при рН = 4 и при pH = 10 на воздухе?
Задача 3 (80 баллов)
Вы находитесь на косе Тузла, разделяющей Черное море (слева) и Азовское море (справа). Рассчитайте разность потенциалов
Елев – Еправ, если для измерения использована а) пара хлор-серебряных электродов, б) пара Na+
селективных электродов. Содержание NaCl в морской воде составляет 18.5 г и 12.0 г на 1 л воды соответственно. Роль солевого моста выполняет
Керченский пролив. Считайте, что минерализация морской воды обеспечивается исключительно хлористым натрием.
Задача 4 (80 баллов)
Железную деталь покрывают краской, состоящей из порошка кадмия. Возможно ли приготовить краску из такого ультрадисперсного порошка кадмия,
при использовании которого не будет происходить коррозионного разрушения детали во влажной среде в присутствии кислорода.
E0(Cd2+/Cd) = - 0,403 В, E0(Fe2+/Fe) = - 0,447 В отн. Н.В.Э.,
ρCd = 8,65 г/см3,
МCd = 112,41 г/моль, σ Cd ≈ 0,8 Дж/м2
Примечание. Коррозия происходит из-за протекания двух полуреакций - анодной Me -> Men+ + ne– и катодной O2 + 4H+ +4e– -> 2H2O (E0 = 1, 23 В отн. Н.В.Э.).
|
Задача 5 (80 баллов) |

|
Известно, что:
Задача 6 (дополнительная, 100 баллов, но при условии, что в сумме не более 400 баллов)
При изучении адсорбции азота, обнаружено, что при T = 273 К и давлении азота 4,5 Торр, масса углеродного сорбента увеличивается по сравнению
с исходной на 22,4 мг, а при давлении 18,6 Торр - на 84,4 мг. Предполагая, что адсорбция следует изотерме Ленгмюра, определите степень заполнения
поверхности сорбента при давлении азота 40 Торр?
Задача 1 (80 баллов)
Рассчитайте равновесное парциальное давление аммиака, если его синтез проводят из азота и водорода при H2:N2 = 3
при постоянном давлении 160 атм и температуре 700 K. Зависимостью теплоемкости от температуры можно пренебречь. При расчете учтите, что коэффициенты
летучести аммиака, водорода и азота для равновесного состава смеси в условиях реакции составляют соответственно 0,93, 0,95 и 0,96.
|
кДж/моль |
Дж/(моль.) |
Дж/(мольК) |
|
|
H2 NH3 |
0 – 45,9 |
130,7 192,8 |
28,8 35,7 |
Задача 2 (80 баллов)
При температуре 400 K получена равновесная газовая реакционная смесь A2 и А, в которой оба вещества представлены в равных мольных
количествах. Суммарное давление полученной смеси равно 2 бар. Определите энтальпию диссоциации А2, если известно, что после изохорного
нагревания до температуры 500 K количество молей димера А2 в новой равновесной смеси уменьшилось в два раза.
Задача 3 (80 баллов)
Замечено, что в диапазоне температур от 10°С до 25°С давление насыщенных паров воды приблизительно следует правилу: “сколько градусов – столько
мм рт. ст.”. Оцените теплоту испарения воды и температуру кипения воды при атмосферном давлении.
Задача 4 (80 баллов)
Коэффициенты активности γi компонент бинарного раствора описываются уравнениями
типа ln(γi)= bi /T, где b1 = 35 К и b2 = 65 К.
Приготовлен эквимолярный раствор. Рассчитайте молярную энтропию и молярную энтальпию смешения. Определите температуру полученного раствора,
приняв исходную температуру обеих компонент (до смешения) равной 20 оС. Известно, что мольная теплоемкость c p бинарного
эквимолярного раствора постоянна и равна 5R.
Задача 5 (80 баллов)
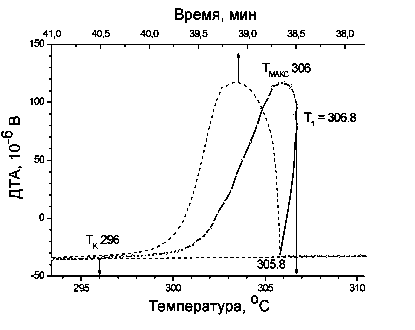
На рисунке приведен фрагмент термической кривой ДТА охлаждения NaNO3, содержащий эффект кристаллизации соли из расплава.
Пунктиром отмечена зависимость сигнала ДТА от времени (верхняя ось абсцисс). Скорость охлаждения – 5 К/мин.
Оцените размер первичных зародышей твердой фазы, если известно, что теплота плавления NaNO3 составляет 16 кДж/моль, а коэффициент поверхностного натяжения для тв. NaNO3 в контакте с расплавом можно полагать равным 0,35 Дж/м2. Плотность NaNO3 = 2,26 г/см3, молярная масса 85 г/моль.
Задача 6 (дополнительная, 100 баллов, но при условии, что в сумме не более 400 баллов)
Существование в системе уран–ртуть трех кристаллических соединений (UHg2, UHg3 и UHg4) было установлено
Рэндлом и Вилсоном (Acta Crystallogr. 1949. Vol. 3. P. 148–150). Используя данные таблицы, постройте Т–х диаграмму в диапазоне температур 250–400 К).
Известно, что Тпл урана 1403 К, Тпл ртути 234 К, твердые растворы в системе не образуются. Также известны термодинамические
характеристики реакций образования соединений U–Hg из α–урана и жидкой ртути
|
|
|
|
|
UHg3 UHg4 |
– 63,55 – 78,01 |
– 46,73 – 66,40 |