3.1. Фазовые равновесия в однокомпонентных системах.
Фазовые переходы I и II рода. Соотношение Клапейрона - Клаузиуса. Равновесие “пар - жидкость” и “пар-твердая фаза”. Равновесие “твердая фаза-твердая фаза”. Равновесие “расплав - твердое тело”. Критическое состояние вещества. Примеры фазовых равновесий (диаграмм) в однокомпонентных системах. Правила Трутона.
3.2. Фазовыеравновесия в двух- и многокомпонентных системах
Парциальные молярные величины. (Однородные функции первого порядка, теорема Эйлера.) Условия равновесия в многофазных многокомпонентных системах. Правило фаз Гиббса. Уравнение Гиббса-Дюгема. Функции смешения идеальных и неидеальных смесей: энтропия, энтальпия, потенциал Гиббса и объем смешен ия. Избыточные функции смешения. Критерий Редлиха - Кистера
3.3. Фазовые равновесия «жидкость - пар» и «жидкость - жидкость» в двух- и многокомпонентных системах.
Классификация растворов: совершенные (идеальные), предельно-разбавленные, регулярные, атермальные. Законы Рауля и Генри. Законы Коновалова. Основные типы диаграмм равновесия “жидкость - пар”. Химический потенциал компонента в растворе, различные типы используемых стандартных состояний. Предельно разбавленные растворы. Равновесие “пар - жидкость” в системе двух несмешивающихся жидкостей или жидкостей с ограниченной растворимостью. Расслоение регулярного раствора. Равновесия в растворах нелетучих веществ в летучих растворителях (бинарный раствор - чистый компонент).
3.4. Равновесия «жидкость - твердое тело» в двух- и многокомпонентных системах.
Основные типы диаграмм равновесия двухкомпонентных систем “жидкость - твердое тело”. Уравнение Шредера. Литостатическое давление, сила кристаллизации. Коллигативные свойства: эбуллиоскопия, криоскопия, осмос. Равновесия в системах с клатратами (на примере газовых гидратов). Некоторые представления о фазовых равновесиях в трехкомпонентных системах.
3.5. Осмос
110. (1/2-00).* Зависимость температуры плавления Sn от давления (в бар)
передается выражением t(&3176;С) = 231,8 + 0,0032(P–1).
Найти плотность твердого олова ρ
тв, учитывая, что Qпл = 7,2 кДж/моль и
ρж = 6,988 г/см3. Молекулярная масса олова 119.
Решение
111. (1/2-05). При 1 бар, 125оС твердые модификации селен (1) и селен (2) равновесно сосуществуют. Энтропии Se(1) и Se(2) равны соответственно 31 и 42 Дж/К.моль. Полагая теплоемкости этих двух фаз равными, вычислить изменения энергии Гиббса при переходе Se(1) → Se(2) при 25° С. Какая фаза селена устойчива при 25° С: Se(1) или Se(2)?
112. (2/2-06). При давлении 1 атм довели температуру 1 моля кристаллического нафталина до температуры плавления. Какое количество тепла необходимо подвести извне для перевода полученного нафталина в жидкое состояние? Известно, что температура плавления нафталина зависит от давления (P, атм) следующим образом:
t° C = 79,8 + 0,0373·P + 1,9·10–6·P2.
Разность мольных объемов жидкого и твердого нафталина равна
Δ V = 18,69 см3/моль.
113. (3/2-97). Давление насыщенного пара (бар) над жидким йодом описывается температурной зависимостью
lgP = –3212/T – 5,193 lgT + 23,705.
Найти теплоемкость газообразного йода, если теплоемкость жидкого йода при температуре кипения 114 °С равна 80,26 Дж/моль·К.
114. (3/Э-01). Давление пара ртути выражается уравнением
lg(Р/торр) = –3328/T – 0,848 lgT + 10,53.
Определить теплоту испарения ртути при температуре кипения (356,66 °С) и удельную теплоемкость жидкой ртути.
115. (1/2-08). Зависимости давления насыщенного пара для твердой и жидкой муравьиной
кислоты (в мм рт. ст.) от температуры выражаются уравнениями:
Рассчитать теплоты испарения, сублимации и плавления. Рассчитать энтропии испарения и сублимации в нормальных точках испарения и сублимации. Рассчитать координаты тройной точки.
116. (3/Э-08). Замечено, что в диапазоне температур от 10 ° С до 25 ° С давление насыщенных паров воды приблизительно следует правилу: "сколько градусов – столько мм рт. ст.". Оцените теплоту испарения воды и температуру кипения воды при атмосферном давлении.
117. (2/2-03). По мотивам книги Роберта Хайнлайна "Фермер в небе": "Во время полета давление было десять фунтов; теперь капитан Хэтти спустила его до трех, то есть до нормального давления на Ганимеде. Ясно, что трех фунтов кислорода вполне достаточно для жизни; на Земле его, кстати, не больше – остальные двенадцать фунтов приходятся на долю азота. Но когда давление падает так внезапно, вы начинаете судорожно хватать ртом воздух….".
Ганимед – спутник Юпитера, сила тяжести ~ 1/3 земной.
Удастся ли колонистам планеты Ганимед сварить куриное яйцо? Если нет, предложите свой способ,
используя подручные средства. Ответ обоснуйте. Температура денатурации белка 62 °С.
|
|
|
|
|
Н2О (ж) Н2О (г) |
–285,83 –241,82 |
69,95 188,84 |
75,3 33,6 |
118. (2/2-04). Можно ли высушить белье при температуре –10о С в зимнем приморском городе на открытом воздухе? В этом городе при –10° С влажность воздуха, приведенная в виде давления насыщенных паров воды, колеблется в интервале 2,00 – 2,10 торр. Известно, что:
а) белье всегда "замерзает" при указанной температуре;
б) изменение энергии Гиббса для процесса Н2О(ж., –10 °С) → Н2О(тв., –10 оС) составляет –212,4 Дж/моль;
в) при –10 °С равновесное давление насыщенных паров над жидкой водой равно 2,149 торр.
119. (1/2-01). Сколько тонн воды может испариться с 1 км2 влажной земли в ясный безветренный летний день, если считать, что лимитирующий фактор – поступление солнечного тепла, которое составляет в среднем 4,18 Дж/(с· см2) в течение 8-часового дня?
Какой минимальный объем воздуха нужен, чтобы вместить это количество воды при температуре почвы и воздуха 25 °С? Давление насыщенного пара воды при 11,3 °С равно 10 торр, а теплота испарения 2433 Дж/г.
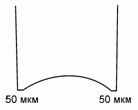 120. (3/Э-06). Коньки, заточенные "под желобок",
имеют толщину острия лезвия около 50 мкм.
120. (3/Э-06). Коньки, заточенные "под желобок",
имеют толщину острия лезвия около 50 мкм.
Оцените температуру плавления льда под спортсменом весом 70 кг на коньках длиной 30 см. Плотность воды 1 г/см3, льда – 0,9 г/см3. Молекулярная масса воды 18 г/моль .
121. (6/2-01).Оцените температуру, при которой максимальна плотность насыщенных паров серы Ткип(S) = 444.6 °C; Tкр(S) = 1040 °C; ΔиспH = 2200 кал/моль. Считать, что ΔиспH не зависит от температуры, а вещество в газовой фазе подчиняется уравнению состояния идеального газа.
122. (5/Э-97). Состояние воды в широком диапазоне температур и давлений достаточно хорошо описывается уравнением Ван-дер-Ваальса:
Оценить по этим данным параметры критического состояния воды (PK, TK, VK). Какой термодинамической вариантностью характеризуется эта точка?
123. (2/2-96). Какова термодинамическая вариантность системы, содержащей MgCO3, MgO и CO2 при условии, что:
а) химического взаимодействия компонентов не происходит (химическое равновесие "отключено");
б) химическое равновесие возможно без ограничений на состав системы;
в) как б), однако твердые фазы могут дополнительно подвергаться действию большого механического давления.
124. (1/2-04). Определить число степеней свободы (вариантность) системы: Aтв + раствор А жидкости В. Как изменится вариантность системы, если она находится в равновесии со своей газовой фазой? Как изменится вариантность системы, если в растворе вещество А частично распадается на ионы по реакции А → X+ + Y–?
125. (4/Э-94). В закрытом лабораторном эксикаторе были оставлены два открытых стакана, один – с водным раствором HCl, другой – с водным раствором NaOH. Что произойдет, если в эксикаторе установится термодинамическое равновесие? Ответ обоснуйте. Как изменится ответ, если эксикатор предварительно вакуумирован?
126. (6/П-94,99). В герметично закрываемый сосуд поместили стакан А с 4 молями чистой воды, стакан В с 6 г сахарозы в 2 молях воды и стакан С с 12 г сахарозы в 3 молях воды. Определите состав равновесной системы при 310 К, допустив, что объем газовой фазы пренебрежимо мал. Изменится ли состав равновесной системы, если в сосуд вносится дополнительно 0,75 моля минерального адсорбента, не образующего водорастворимых соединений, но способного связывать воду в стехиометрическом соотношении 1 : 2?
127. (5/Э-96). В откачанном эксикаторе небольшого объема находится стакан с разбавленным водным раствором NaCl. Сколько термодинамических степеней свободы имеет такая система? Как изменится ответ, если в стакане будет разбавленный водный раствор глюкозы? Как изменятся ответы, если эксикаторы не были предварительно откачены?
128. (2/2-96). В термостатированный эксикатор при температуре 330 К помещают три стакана А, В, С объемом 75 мл, содержащие соответственно:
А: 1 г NaCl в 25 мл воды,
В: 0,5 г NaCl и 0,5 г AgCl в 25 мл воды,
С: 1 г NaCl в 50 мл воды.
Как будет выглядеть система при достижении равновесия? Сколькими степенями свободы обладает система? Объемом газовой фазы можно пренебречь.
129. (4/Э-00). Плотность 60 %-го (вес. %) водного раствора метилового спирта при 293 К равна 0,8946 г/см3. Парциальный мольный объем воды в этом растворе равен 16,8 см3/моль. Определить парциальный мольный объем спирта в данном растворе.
130. (2/2-05). В таблице приведена зависимость удельной теплоемкости водного раствора KCl в зависимости от концентрации при 18 oС. Оцените парциальные мольные теплоемкости компонентов раствора при m = 1,11.
|
Ср, Дж/(г*К) при концентрации KCl m, моль/кг Н2О |
|||
M |
2,22 |
1,11 |
0,555 |
Cр |
3,46 |
3,78 |
3,97 |
131. (5/2-03). Рассчитайте КПД адсорбционной установки выделения кислорода из воздуха, если ее производительность составляет 0,5 м3 О2 / час при Т = 25 °С и стандартном давлении, а потребляемая мощность 1,1 кВт. Содержание кислорода в воздухе 21 об.%. При решении задачи предположить, что кислород полностью отделяется от остальных газов.
132. (3/Э-95). Какую минимальную работу следует затратить на извлечение одного моля первого вещества из 10 молей идеальной смеси четырех веществ с молярными долями 0,1, 0,4, 0,3 и 0,2 соответственно.
133. (4/Э-96). Парциальные давления паров бензола и толуола над идеальным эквимолярным раствором составляют при 25 C 48 и 15 торр соответственно.
а) При каком составе раствора (в мол. долях) раствор будет кипеть при Т = 25 &176;С и р = 75 торр?
б) Какую минимальную работу необходимо затратить для разделения 1 моля паровой фазы над раствором "а" на исходные компоненты?
в) Возможно ли кипение раствора бензол-толуол при 25 °С и 100 торр; при 60 °С и 500 торр?
Известно, что при 25 °С для бензола и толуола соответственно ΔНпл = 9,9 и 6,64 кДж/моль, ΔНисп = 33,85 и 38,1 кДж/моль
134. (1/2-06). Этанол и метанол п1ри смешении образуют раствор, близкий к идеальному. При 20 °С давление пара над чистым этанолом равно 44,5 торр, а над чистым метанолом – 88,7 торр. Рассчитайте давление пара над 50 % (вес.) раствором, а также состав пара над этим раствором при 20 °С. Определите минимальную работу, необходимую для разделения одного моля паровой фазы на исходные компоненты?
135. (1/2-98). Стандартные теплоты и нормальные температуры кипения бензола и воды равны 33,90 и 44,02 кДж/моль и 80 и 100 °С соответственно. Определить равновесный состав пара (в мольных долях) над бинарной смесью указанных взаимно несмешивающихся веществ при 73 °С. Для приготовления смеси взяты 0,25 моля бензола и 0,45 моля воды.
136. (1/2-02). Смесь метилкарбинола и воды при атмосферном давлении кипит при 87 °С.
Теплоты испарения чистых компонентов составляют
137. (2/2-99). Равновесная система представлена газовой фазой и кристаллическими p-бензохиноном и антраценом, помещенными в насыщенный раствор этих веществ в гексане. Какова вариантность системы? Как изменится давление насыщенных паров p-бензохинона, если к исходной системе добавить кристаллическую бензойную кислоту: состояние насыщения по бензойной кислоте (случай I) не будет, или (случай II) будет достигнуто? Обоснуйте ответы.
138. (3/2-06). При температуре 298 К давления насыщенных паров над кристаллическими d-камфорой и нафталином равны 0,328 и 0,0857 торр соответственно. Приготовлен насыщенный раствор указанных веществ в метиловом спирте таким образом, что в нерастворенном осадке содержится 0,05 моля d-камфоры и 0,01 моля нафталина, а мольные доли этих веществ в насыщенном растворе равны 0,32 и 0,08. Определите отношение давлений насыщенных паров этих веществ над полученным раствором. Как изменится отношение давлений, если количество нерастворенной камфоры уменьшить до 0,01 моля. Какова вариантность равновесной системы, представленной газовой фазой и насыщенным раствором?
139. (4/2-99). Определите состав пара и жидкости смеси SnCl4-CCl4, образующих совершенный раствор, при давлении 1 бар и температуре 100 °С, при которой давление насыщенных паров чистых SnCl4 и CCl4 равны 497 и 1450 торр соответственно.
Температура кипения при Р = 1 бар для SnCl4 составляет 114° С, а для CCl4 – 77 °С.
Построить схематично диаграммы состояния в координатах Р-х; Т-х, указав точки, по которым диаграмма строилась.
140. (5/2-94). Газовые гидраты (например, метана) представляют собой твердые соединения, в которых гидратообразователь (например, метан) входит в “правильные” плоскости, образуемые молекулами воды. Полагая, что молекулы метана могут равновероятно войти в любую из этих плоскостей, которые до этого являлись пустыми, рассчитайте мольную энтропию гидратированного метана, связанную с гидратообразованием, в зависимости от степени заполнения, q , газового гидрата метаном. Для простоты считать, что предельный состав газового гидрата соответствует формуле CH4× 6H2O.
141. (1/3-94). Равновесное давление метана над жидким метаном составляет 25 атм при –110 °С и 11,8 атм при –120 °С. Оцените растворимость метана в идеальном растворителе при 25 °С и парциальном давлением 1 атм.
142. (2/2-01). При 40 °С растворимость воды в анилине и анилина в воде равны 5 вес. %. Оценить нормированные на чистый компонент коэффициенты активности компонентов в данных растворах. Каким будет давление пара воды над системой, содержащей 3 моля воды и 3 моля анилина, если давление пара над чистой водой при этой температуре равно 55,3 торр.
143. (4/Э-02). В препаративной практике органической химии нередко перед разделением смеси нерастворимых в воде органических веществ методом перегонки в смесь добавляют воду. Поясните результат и полезность этого приема, приведя соответствующие диаграммы.
144. (3/Э-07). Рассчитайте фазовую диаграмму “температура-состав” системы вода-бромбензол, компоненты которой не смешиваются в жидком состоянии, при общем давлении в системе 760 торр. Сколько грамм воды потребуется для перегонки 1 моля C6H5Br?
ln P0H2O (торр) = – 5013,5/Т + 20,074,
ln P0C6H5Br (торр) = – 4761,6/Т + 17,727,
Атомная масса Br = 79,9.
145. (5/2-99). Оценить растворимость шестифтористого урана (в граммах) при 30 °С в 1000 мл жидкого растворителя (r = 1,2 г/см3, м.в. 156), если давление пара над твердым и жидким UF6 даются уравнениями:
lgPтв(торр) = 10,648 – 2559,5× Т–1,
lgPж(торр) = 7,54 – 1511,3× Т–1,
tпл(UF6) = 64 °C, атомная масса U 238.
146. (4/2-08). В индивидуальном состоянии жидкости А и В имеют одинаковые температуры кипения и энтальпии испарения, равные 123,0 oC и 16,62 кДж/моль соответственно. Жидкости не смешиваются при любом их соотношении. Приготовлена двухфазная смесь с использованием 1 моля жидкости А и 4 молей жидкости В. При какой температуре закипит смесь? Каким будет состав дистиллята?
147. (3/2-04). Для двухкомпонентного раствора мольная энергия Гиббса смешения имеет вид D GM = RT [xAlna xA2 + xBlna xB2], где a = 650 Дж/моль. Мольная теплоемкость этого раствора описывается уравнением ср = 24,85 + 1,5xB (Дж/моль.К) и практически не зависит от температуры. Смешивают вещества А (4 моля) и В (6 молей), взятые при температуре 20 ° С. Определите температуру полученного раствора.
148. (2/2-98). Термодинамический потенциал для моля твердого раствора железо-кремний описывается выражением
G = xFem oFe + xSim oSi + RT(xFelnxFe + xSilnxSi) – 167000xFexSi.
Найти выражение для химических потенциалов отдельных компонентов.
149. (2/2-95). На океаническом дне вблизи вулканических зон вода представляет собой насыщенный раствор углекислого газа. Оценить, какой объем углекислого газа выделится из 1 л такой воды при ее подъеме с глубины 5 км, где она находилась при температуре 10 ° С. Считать, что раствор является идеальным, в то время как коэффициент летучести углекислого газа на указанной глубине равен 0,4. Коэффициент Генри для углекислого газа в морской воде принять равным 5.10–3 моль СО2/(1000 г Н2О× бар).
150. (6/2-02). Полагая, что существует равновесие между атмосферным кислородом и кислородом, растворенным в морской воде, оценить равновесную концентрацию кислорода в Марианской впадине (13 км), если давление О2 над поверхностью воды составляет 20 % от атмосферного. Температура воды во впадине 2 °С. Изменением температуры с глубиной и изменением мольного объема жидкого O2 при повышении давления пренебречь. Константа Генри для кислорода при указанной температуре Kг = 3,74.10–5 атм–1. Плотность жидкого кислорода принять равной 0,1 г/см3.
151. (4/Э-08) Коэффициенты активности g i компонент бинарного раствора описываются уравнениями типа
ln(g i)= bi /T, где b1 = 35 и b2 = 65.
Приготовлен эквимолярный раствор. Рассчитайте молярную энтропию и молярную энтальпию смешения. Определите температуру полученного раствора, приняв исходную температуру обеих компонент (до смешения) равной 20 ° С. Известно, что мольная теплоемкость сP бинарного эквимолярного раствора постоянна и равна 5R.
152. (4/2-07). Зависимость коэффициента активности вещества А от состава бинарного жидкого раствора, образованного веществами А и В, описывается уравнением
ln gA = axB2 + bxB3.
Определите значения констант Генри для веществ А и В в бинарной системе А-В, если известны давления насыщенных паров над чистыми компонентами.
153. (4/2-03).* Равновесное давление пара над сконденсированным газом В равно 38 бар
при 22 °С. Зависимость коэффициента активности нелетучего растворителя А от состава бинарного
жидкого раствора, образованного веществами А и В, при этой температуре описывается уравнением
Решение
154. (4/2-06). Для расплава PbBr2 (компонент 1, tпл = 373 ° C) и ZnBr2 (компонент 2, tпл = 392 ° C) при 500 ° С зависимость коэффициента активности g 1 от состава имеет вид lng 1 = 0,40 x24. Предложите методику приготовления расплава, для которого g 1 = g 2.
155. (6/2-04). Зависимость мольной энергии Гиббса смешения жидких веществ А и B от состава раствора имеет вид
D
GM= RT [a
xAxB + xAlnxA + xBlnxB].
Равновесный пар над эквимолярным раствором этих веществ содержит 20 мольных процентов компонента А, при этом парциальное давление А равно 50 торр. Зная, что давление пара чистого компонента А равно 200 торр, определите константу Генри для компонента В.
156. (4/Э-97). Коэффициент активности бензола (g 1) в смеси с н-бутилсебацинатом можно рассчитать по уравнению:
где а = –1,816; с = –0,950; х2 – мольная доля н-бутилсебацината. Рассчитать коэффициент активности н-бутилсебацината в смеси, в которой его мольная доля составляет 0,1.
157. (7/П-02). Система содержит 1 моль вещества А и 1 моль вещества B. Известно, что выражение коэффициента активности вещества А для раствора В в А имеет вид
ln(g A) = –2{xB + ln(1 – xB)}.
Найти равновесное состояние системы (состав сосуществующих фаз), если известно, что в системе газообразные и твердые фазы отсутствуют.
158. (2/2-08). Известно, что парциальный мольный объем K2SO4 в водном растворе при 25˚oC описывается уравнением
где m – моляльность исследуемого раствора. Мольный объем чистой воды при 25˚oC примите равным 18,079 см3. моль–1. Определите объем раствора, приготовленного из 1 моля сульфата калия и 1000 г воды.
159. (3/2-01). Для бинарного раствора зависимость давления насыщенного пара одного из компонентов от состава раствора описывается уравнением
P1 = P1o x1 exp(bx23).
Найти работу, которую необходимо совершить для извлечения одного моля второго компонента из очень большого количества эквимолярного раствора при температуре 300 К и b = 0,1.
160. (1/2-99). Смешение 1 моля вещества А и 9 молей вещества В, проведенное при 298 К,
сопровождалось выделением 1800 Дж тепла. Определите минимальную работу, необходимую
для разделения одного моля гомогенного эквимолярного раствора указанных веществ, если известно,
что разделение проводится при 320 К, а коэффициенты активности и мольные доли и
ндивидуальных компонент связаны соотношением
161. (3/2-05).* Найти работу разделения эквимолярной бинарной неидеальной смеси на чистые компоненты при 298 К и атмосферном давлении, если известно, что логарифм коэффициента активности γ1 для этой смеси зависит от состава согласно уравнению:
162. (3/2-00). Зависимость давления насыщенного пара чистой жидкой меди (в бар) от температуры описывается уравнением
lg Po = –16050/T + 5,666.
Определить парциальную мольную теплоту растворения меди при 1823 К в растворе Fe-Cu (концентрация меди 89,5 мол. %, свойства раствора близки к регулярным), если давление насыщенного пара меди над этим раствором равно 6,74× 10–4 бар.
163. (4/Э-98). Экспериментально установлено, что парциальные давления паров углеводорода А (PА, бар) и углеводорода В (PВ, бар) над бинарным раствором этих компонент при температуре 310 К описываются уравнениями:
ln(PА) = –1,67 + ln(xА) + xВ2 (1 + 2xВ)
ln(PВ) = –2,04 + ln(xВ) + 2xА2 (1 – xВ)
где xА и xВ – мольные доли веществ А и В соответственно. Проверьте эти уравнения на взаимную согласованность.
164. (3/2-99). Азеотропическая точка типа “минимум” на фазовой диаграмме кипения двухкомпонентного раствора (раствор гомофазный) определена координатами t = 82,6 °С, x2 = 0,4. Для этой точки известны значения g 2ж = 2,00 и (¶ g 2ж/¶ x2) = 0,6. Определите парциальные давления компонент над кипящим азеотропом. Определите значения g 1ж и (¶ g 1ж/¶ x1) в азеотропической точке. Известны давления насыщенных паров и теплоты кипения индивидуальных веществ при t = 82,6 °С: Pо01 = 760 торр, Pо02 = 380 торр, D Н1° = 8,64 кДж/моль, D Н2° = 10,12 кДж/моль.
165. (3/2-03). Сероуглерод и хлористый метилен при содержании CS2 35 вес. % образуют азеотропную смесь с температурой кипения 35,7 °С. Найти коэффициенты активности компонентов в жидкой фазе. Газовую фазу считать идеальной.
|
Температура кипения при давлении насыщенного пара, °С |
||
|
400 мм. рт. ст. |
760 мм. рт. ст. |
|
|
CS2 |
28,0 |
46,2 |
|
CH2Cl2 |
22,8 |
40,0 |
166. (2/2-02). Реагенты А (“1”) и В (“2”) образуют регулярный раствор, в котором
167. (5/2-01). В водном растворе уксусная кислота существует в мономерной форме,
а в неполярных жидкостях (как бензол) – в форме димеров. Показать, что для коэффициента
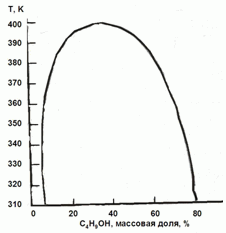
К распределения кислоты между водой и бензолом справедливо выражение
168. (3/2-96). Кипение системы из двух взаимно нерастворимых жидкостей характеризуется
эффективным значением энтальпии испарения
169. (4/2-96). Зависимость давления насыщенного пара некоторого углеводорода от температуры приведена в таблице
|
T, °C |
–10 |
0 |
10 |
20 |
30 |
|
P, торр |
40 |
85 |
200 |
500 |
1050 |
Его растворение в глицерине при 20 °С и давлении 50 торр приводит к получению раствора с мольной долей глицерина 0,95. Зависимость коэффициента активности глицерина от мольной доли углеводорода х описывается уравнением lng
гл = ах2.
Определите значение коэффициента а.
170. (2/3-94). Парциальный мольный объем растворенного компонента в разбавленном растворе некоторого растворителя описывается уравнением V2 = a + bm + cm2, где m – мольная концентрация растворенного вещества, a, b, и с – константы. Найдите парциальный мольный объем растворителя V1 как функцию m. Считать, что молекулярная масса растворителя М1 г/моль, а его плотность – r 1 г/см3. Размерность мольных объемов – см3.
171. (3/2-95). Вычислить изменение молярной энтропии серебра
в то время как зависимость давления насыщенного пара чистого серебра выражается уравнением:
172. (1/2-07) Азот медленно пропускают через раствор 3 г нелетучего вещества в 200 г бензола, а затем через чистый бензол. Через некоторое время вес раствора уменьшился на 2,154 г, а чистый бензол потерял в весе 0,016 г. Чему равен молекулярный вес растворенного вещества?
173. (4/Э-04). Оцените, при какой температуре кипит раствор 1,45 г дихлоруксусной кислоты в 56,9 г четыреххлористого углерода?
А на самом деле точка кипения повышается на 0,52 K...
Чем, по-вашему, объясняется расхождение с экспериментом?
Tкип, ° С |
ΔНпл, кДж.моль–1 | М, г.моль–1 |
|
ССl4 |
76,6 | 29,8 | 153,8 |
С2HСl2OOH |
194 | 48,2 | 128,9 |
174. (3/Э-94). Температура кипения диметилового эфира при давлении 1,01 бар составляет 25,2 °С. При растворении 10,94 г некого нелетучего вещества в 100 г этого эфира давление пара эфира при 15,3 °С составило 0,598 бар. Вычислить молекулярную массу растворенного вещества, если известно, что теплота испарения чистого эфира составляет 17,28 кДж/моль.
175. (1/2-95). Изобразить качественно фазовые диаграммы “давление – состав” и “температура кипения – состав” для смеси бромбензола с водой, которые нерастворимы друг в друге. Указать, чему соответствует каждая из областей нарисованных диаграмм. Сколько воды потребуется для перегонки 100 г бромбензола с водяным паром при 1 атм и 368,3 К, если парциальное давление воды при этом составляет 0,852 атм.
176. (6/2-05). Какие из представленных ниже диаграмм “газ – жидкость” принципиально возможны, а какие нет? Еcли нет, то почему?
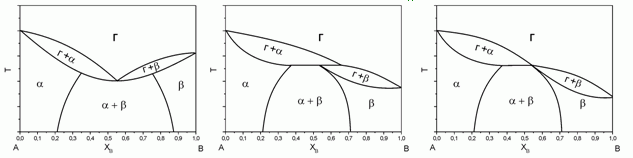
 177. (3/2-08).
На основании фазовой диаграмма “жидкость – пар” для системы
H2O-C4H9OH оцените коэффициенты активности воды в сосуществующих
фазах при 350 К.
177. (3/2-08).
На основании фазовой диаграмма “жидкость – пар” для системы
H2O-C4H9OH оцените коэффициенты активности воды в сосуществующих
фазах при 350 К.
Каким будет давление пара воды над системой, содержащей 3 моля H2O и 2˚моля C4H9OH?
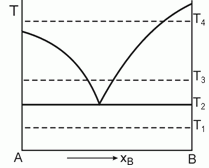 178. (2/Э-01).
Дайте интерпретацию приведен-ной диаграмме фазового равновесия, полученной при анализе смесей двух веществ А и В, являющихся жидкостями при температуре Т1.
178. (2/Э-01).
Дайте интерпретацию приведен-ной диаграмме фазового равновесия, полученной при анализе смесей двух веществ А и В, являющихся жидкостями при температуре Т1.
Постройте ожидаемые диаграммы фазового равновесия в координатах Р-x при температурах Т1, Т2, Т3 и Т4.
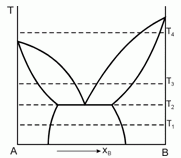 179. (5/2-97). Дайте интерпретацию приведен-ной диаграмме фазового равновесия, полученной при анализе смесей двух веществ А и В, являющихся жидкостями при температуре Т1. Постройте ожидаемые диаграммы фазового равновесия в координатах Р-Т при температурах Т1, Т2, Т3 и Т4.
179. (5/2-97). Дайте интерпретацию приведен-ной диаграмме фазового равновесия, полученной при анализе смесей двух веществ А и В, являющихся жидкостями при температуре Т1. Постройте ожидаемые диаграммы фазового равновесия в координатах Р-Т при температурах Т1, Т2, Т3 и Т4.
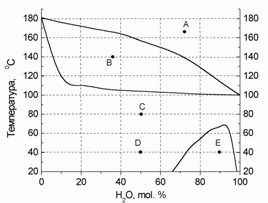 180. (4/2-05).* На рисунке приведена диаграмма состояния “температура – состав” для системы “вода – фе-нол” при давлении 760 торр. Определите, какие и какого состава фазы присутствуют в системе в точ-ках А – Е. Нарисуйте схематично диаграмму при P = 100 торр. Для воды D
испН = 40,66 кДж/моль (tкип = 100 оС).
180. (4/2-05).* На рисунке приведена диаграмма состояния “температура – состав” для системы “вода – фе-нол” при давлении 760 торр. Определите, какие и какого состава фазы присутствуют в системе в точ-ках А – Е. Нарисуйте схематично диаграмму при P = 100 торр. Для воды D
испН = 40,66 кДж/моль (tкип = 100 оС).
Для фенола D
испН = 47,97 кДж/моль (tкип = 181,9 оС).
Решение
181. (4/Э-05). Природа активного компонента Сu-Zn катализатора синтеза метанола вызывает много дискуссий. Одной из гипотез является образование Сu-Zn бронзы при обработке в восстановительной среде. Оценить равновесный состав металлических частиц катализатора Cu0/ZnO после их обработки в токе смеси 0,1 % H2O в водороде при атмосферном давлении и 500 К в предположении, что Сu-Zn бронза представляет собой идеальный раствор атомов цинка в металлической меди.
Процесс восстановления оксида цинка ZnO + H2 = Zn0 + H2O при 500 К характеризуется ΔrS0 = 57 Дж/(моль К) и ΔrH0 = 110 кДж/моль.
182. (6/2-95). Рассчитать изменение температуры замерзания воды, вызванное растворением воздуха в ней при 1 атм. (Воздух состоит из 79 % N2 и 21 % O2.) Константы Генри для О2 и N2 в воде при 273,2 К равны соответственно 2,51× 104 и 5,38× 104 атм. D НплН2О = 6029 Дж/моль.
183. (5/2-96). Определите формулу углеводорода на основании следующих данных: из 0,2 г вещества образуется 0,653 г СО2 и 0,320 г Н2О. Температура замерзания раствора, содержащего 0,09056 г вещества в 0,01 кг бензола, ниже Тпл. бензола на 0,354°. Ккриос. бензола = 5,16.
184. (6/Э-98). Раствор, содержащий 1,632 г трихлоруксусной кислоты в 100 г бензола, при охлаждении отвердевает на 0,350 °С ниже, чем чистый бензол. Определить, имеет ли место ассоциация или диссоциация кислоты и в какой степени, если теплота плавления чистого бензола равна 9,95 кДж/моль.
185. (4/2-04). При 50 оС приготовлен насыщенный раствор нафталина в бензоле. Оцените температуру, до которой следует охладить раствор для того, чтобы половина от использованного нафталина выпала в форме кристаллов. Энтальпия плавления нафталина при нормальной температуре его плавления (80.0 oC) равна 19,29 кДж . моль–1. Раствор можно считать идеальным.
186. (5/2-08) Энтальпия плавления нафталина при нормальной температуре его плавления (80,0 oC) равна 19,29 кДж/моль. При температуре 20 ° С проводится эксперимент по приготовлению насыщенного раствора нафталина в гексане. Будет ли получен насыщенный раствор при добавлении 0,48 моля нафталина к 0,72 моля гексана? Какова вариантность системы, включающей насыщенный раствор и равновесную с ним газовую фазу?
187. (3/2-02). К 15,401 г бензола, температура замерзания которого равна 5,400 °С, прибавлено 3,747 г раствора фосфора в бензоле, насыщенного при 18 °С. Точка отвержения полученной смеси оказалась равной 5,155 °С. Считая, что растворенная в бензоле молекула фосфора состоит из 4-х атомов, вычислить растворимость фосфора в бензоле при 18 °С, выразив ее в весовых процентах. Криоскопическая константа бензола равна 5°/моль. Атомная масса фосфора 31.
188. (3/П-94,99). Покажите, что незначительные загрязнения кристаллического вещества обычно приводят к понижению температуры его плавления. Как зависит это понижение от природы кристаллического вещества и примеси? Существуют ли исключения из сформулированного правила?
189. (1/2-97). Какие морозы еще не страшны для перевозки сухого вина на открытых машинах?
Известно, что для воды Δ
испHo = 44 кДж/моль, Δ
плНо = 6 кДж/моль.
190. (3/Э-07). После нагревания смеси 9 молей Cd и 1 моля Bi до некоторой температуры 4,5 моль Сd остались в твердом состоянии, а висмут расплавился полностью. Определите эту температуру, если известно, что компоненты не образуют твердых растворов (растворимость Bi в твердом Cd вблизи Тэвт = 0,03 %). Δ плHCd = 6,23 кДж/моль, tпл Cd = 321,1 ° С, Δ плHBi = 10,9 кДж/моль, tпл Bi = 271,3 ° С.
191. (5/Э-94). Вывести правило рычага для фазовых диаграмм "расплав – твердая фаза".
192. (5/2-98). Двухкомпонентные системы NaCl-AgCl и KCl-AgCl характеризуются неограниченной растворимостью компонентов друг в друге как в жидком, так и твердом состоянии.
tпл AgCl = 456 °С, tпл NaCl = 800 °С,
tпл KCl = 339 °С. Однако смесь KCl-AgCl имеет точку эвтектики,
а смесь NaCl-AgCl – нет.
Построить схематично обе диаграммы в координатах Т-х и оценить
положение точки эвтектики. ΔплНAgCl = 12,7 кДж/моль,
ΔплНКCl = 12,82 кДж/моль.
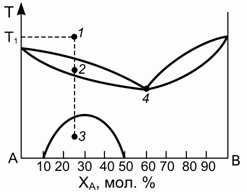 193. (1/2-96). Диаграмма, описывающая равновесие "жидкость – тв.тело" (например, для смеси LiCl-NaCl), имеет вид, представленный на рисунке.
193. (1/2-96). Диаграмма, описывающая равновесие "жидкость – тв.тело" (например, для смеси LiCl-NaCl), имеет вид, представленный на рисунке.
Определить, какие, сколько и какого состава фазы присутствуют в системе в точках 1, 2, 3, 4, если при температуре Т1 было расплавлено 15 молей смеси.
Подсчитать число независимых термодинамических переменных в точках 3 и 4.
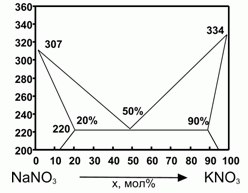 194. (6/2-00). Фазовая диаграмма плавкости
KNO3 – NaNO3 представлена на рисунке.
194. (6/2-00). Фазовая диаграмма плавкости
KNO3 – NaNO3 представлена на рисунке.
Δ Нпл (NaNO3) = 16 кДж/моль; Δ
Нпл (KNO3) = 11,7 кДж/моль; 1 моль механической смеси нитратов К и Na в мольном соотношении 1:1 расплавили и остудили до затвердевания и вновь расплавили. Оценить теплоту плавления смеси при повторном плавлении. Для оценки считать, что теплоемкость нитратов в жидком и твердом состоянии одинаковы, а все растворы - регулярны.
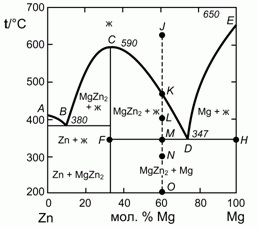 195. (1/2-96). 0,60 моля Mg и 0,40 моля Zn нагрели до 650 °C (точка J на фазовой диаграмме плавкости системы цинк – магний, изображенной на рисунке). Опишите, что будет происходить с этой системой при ее охлаждении до 200 °C (точка О). Каково состояние системы в точках K, L, М и О, а также составы и отношения количества соответствующих фаз?
195. (1/2-96). 0,60 моля Mg и 0,40 моля Zn нагрели до 650 °C (точка J на фазовой диаграмме плавкости системы цинк – магний, изображенной на рисунке). Опишите, что будет происходить с этой системой при ее охлаждении до 200 °C (точка О). Каково состояние системы в точках K, L, М и О, а также составы и отношения количества соответствующих фаз?
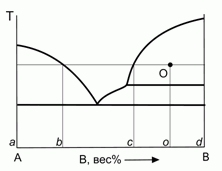 196. (6/2-99). Для фигуративной точки О на диаграмме плавкости бинарной системы с неконгруентным плавлением найти мольную долю вещества, находящегося в разных фазах системы, а также мольные доли компонентов в разных фазах. Ответ пояснить.
196. (6/2-99). Для фигуративной точки О на диаграмме плавкости бинарной системы с неконгруентным плавлением найти мольную долю вещества, находящегося в разных фазах системы, а также мольные доли компонентов в разных фазах. Ответ пояснить.
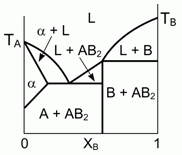 197. (6/2-03). Представленная на рисунке фазовая диаграмма, описывающая особенности
кристаллизации двухкомпонентной жидкости (здесь L-жидкость), не соответствует физико-химическим реалиям.
197. (6/2-03). Представленная на рисунке фазовая диаграмма, описывающая особенности
кристаллизации двухкомпонентной жидкости (здесь L-жидкость), не соответствует физико-химическим реалиям.
Исправьте ошибку. Что представляет собой фаза a ?
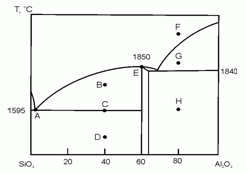 198. (4/Э-06). На рисунке схематично представлена фазовая диаграмма плавления системы оксид кремния – оксид алюминия.
198. (4/Э-06). На рисунке схематично представлена фазовая диаграмма плавления системы оксид кремния – оксид алюминия.
Опишите фазовый состав системы в точках А – H, отмеченных на диаграмме.
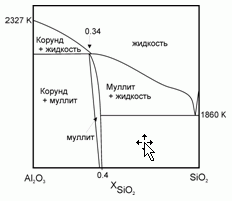 199. (5/Э-05).Плавление муллита 2Al2O3*SiO2 протекает с образованием твердого корунда α-Al2O3 и расплава, близкого по своему составу к муллиту. Известны температура плавления корунда Тпл (α-Al2O3) = 2327 K и теплота его плавления Δ
Hпл (α-Al2O3) = 111 кДж/моль. Полагая, что расплав SiO2–Al2O3 – идеальный раствор, оцените температуру плавления муллита.
199. (5/Э-05).Плавление муллита 2Al2O3*SiO2 протекает с образованием твердого корунда α-Al2O3 и расплава, близкого по своему составу к муллиту. Известны температура плавления корунда Тпл (α-Al2O3) = 2327 K и теплота его плавления Δ
Hпл (α-Al2O3) = 111 кДж/моль. Полагая, что расплав SiO2–Al2O3 – идеальный раствор, оцените температуру плавления муллита.
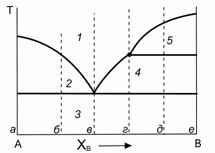 200. (7/Э-00). Некоторая бинарная система с неконгруентным плавлением характеризуется следующей диаграммой плавкости.
200. (7/Э-00). Некоторая бинарная система с неконгруентным плавлением характеризуется следующей диаграммой плавкости.
Дайте качественное пояснение данной диаграмме и природе ее отдельных участков "1"–"5". Нарисуйте качественно вид интегральных и дифференциальных кривых остывания при термическом анализе системы для конкретных составов в точках "а"– "е".
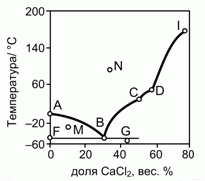 201. (4/2-02). На рисунке приведена фазовая диаграмма плавкости для бинарной системы "вода – CaCl2".
201. (4/2-02). На рисунке приведена фазовая диаграмма плавкости для бинарной системы "вода – CaCl2".
Опишите особенности состава системы в точках A, B, C, D, F, G, I, M и N.
Как называются отмеченные точки B, C, D ?
Молекулярная масса CaCl2 – 111.
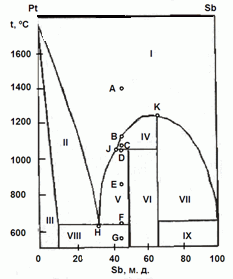 202. (6/2-08).На рисунке приведена фазовая диаграмма
плавкости для бинарной системы "Pt – Sb".
202. (6/2-08).На рисунке приведена фазовая диаграмма
плавкости для бинарной системы "Pt – Sb".
Назовите равновесные фазы и укажите их число в областях I – IX.
Опишите, что будет происходить с системой при охлаждении расплава с содержанием Sb 45 % от 1400 ºС (точка А) до 550 ºС (точка G).
Каково состояние системы в точках B, C, D, E, F? Как называются точки Н, J, K?
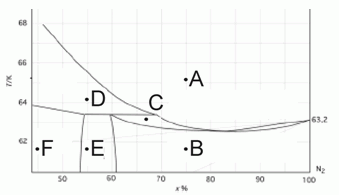 203. (5/2-07).* На рисунке представлена фазовая диаграмма T(x) для бинарной системы "Ar – N2" в области фазовых переходов твердое – жидкость (T указана в К).
203. (5/2-07).* На рисунке представлена фазовая диаграмма T(x) для бинарной системы "Ar – N2" в области фазовых переходов твердое – жидкость (T указана в К).
Опишите фазовый состав в точках А–F.
(по данным: Long H. M., Di Paolo F. S., 1963, Chem. Eng. Prog. Symp. Ser., Vol. 59, p. 30–35).
204. (6/2-06). Чугуном называется сплав железа с углеродом, в котором содержание углерода превышает 2,14 мас. %. При выплавке стали, уменьшения содержания углерода в расплаве достигают окислением его кислородом воздуха. Какого содержания углерода в стали могли достигать в мартеновских печах в 19 веке, если удавалось поддерживать температуру расплава 1450 ° С?
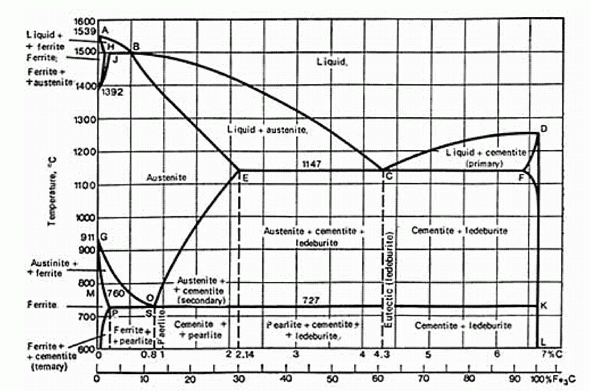
Ferrite (феррит) – α-Fe0; Austenite (аустенит) – γ-Fe0; Cementite (цементит) – Fe3C; Ledeburite (ледебурит) и pearlite (перлит) – названия, принятые для композитных структурных составляющих гетерогенных твердых систем Fe-C, соответствующих на диаграмме эвтектике "С" и эвтектоиду "O".
205. (6/Э-08). Существование в системе "уран – ртуть" трех кристаллических соединений (UHg2, UHg3 и UHg4) было установлено Рэндлом и Вилсоном (Acta Crystallogr. 1949. Vol.3. P. 148–150). Используя данные таблицы, постройте Т-х диаграмму в диапазоне температур 250 – 400 К). Известно, что Тпл урана 1403 К, Тпл ртути 234 К, твердые растворы в системе не образуются. Также известны термодинамические характеристики реакций образования соединений U-Hg из a -урана и жидкой ртути
Соединение |
ΔfH, кДж/моль |
ΔS, Дж/моль*K |
UHg2 |
– 52,72 |
– 37,57 |
UHg3 |
– 63,55 |
– 46,73 |
UHg4 |
– 78,01 |
– 66,40 |
206. (5/3-94). Образование газовых гидратов метана [CH4× 6H2O], представляющих собой термодинамически нестойкие твердые вещества, соответствует уравнению
CH4 + 6H2O = [CH4× 6H2O].
Изобразите качественно диаграмму состояния (фазовую диаграмму) для процесса гидратообразования в координатах "общее давление –температура" (диаграмма Розебома – Штакельберга). Области с сосуществованием твердой фазы метана и газообразной воды можно не рассматривать. Считать, что метан и вода взаимно не растворяются друг в друге. Учесть, что плотность гидрата метана меньше плотности жидкой воды.
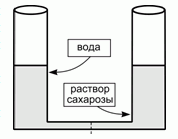
207. (4/2-98). В начальном состоянии одинаковые цилиндрические сосуды высотой 20 см наполовину заполнены водой и 0,001 М водным раствором сахарозы, соответственно. В нижней части сосуды соединяются трубкой, содержащей полупроницаемую для воды мембрану. Опишите равновесное состояние системы. Температура 300 К, плотность раствора сахарозы 1 г/см3, объем соединительной трубки пренебрежимо мал. Изменится ли результат при замене сахарозы на NaCl? Каким количеством степеней свободы обладает равновесная система (ответ обоснуйте)?
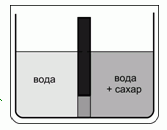
208. (5/Э-01). В равные по объему части сосуда, разделенного перегородкой, которая внизу имеет проницаемую только для воды мембрану, налили одинаковое количество чистой воды, а затем в одном из отсеков растворили сахар в концентрации С. Опишите равновесное состояние системы, если оно устанавливалось в герметичной и термостатированной оболочке, окружающей сосуд. Как изменится равновесие, если оболочка разгерметизирована и система сообщается с окружающим воздухом? Ответ аргументируйте.
209. (5/2-00). Три одинаковых вертикальных цилиндрических сосуда каждый сечением 10 см2 соединены снизу мембранами, проницаемыми для воды. В сосуде A содержится 1 ммоль NaCl, в сосуде C – 2 ммоль NaCl. В сосуд B наливают чистую воду. После установления равновесия разность высот столбов воды в сосудах А и B составила 15 см. Какова разность высот столбов воды между сосудами B и С? Пренебречь влиянием концентрации раствора на его плотность. Температура – 298 K.
210. (5/2-02). Цилиндрический сосуд А сечением 20 см2 помещен в цилиндрический сосуд В сечением 40 см2. Дно сосуда А выполнено из материала, проницаемого для воды. В сосуд В начинают лить 5× 10–3 М раствор NaCl. Сколько раствора можно влить в систему, не переливая края посуды, если высота сосудов составляет 50 см? Влиянием концентрации на плотность раствора пренебречь. Ускорение свободного падения g = 9,8 м c–2.
211. (5/2-04) Плазма человеческой крови замерзает при –0,56oC. Каково ее осмотическое давление при 37 oC, измеренное с помощью мембраны, проницаемой только для воды?
212. (5/2-05) Уксусную кислоту в количестве 10–4 моль растворили в 1 л воды. Уровень полученного раствора при 0 ° С оказался на 2,7 см выше уровня чистой воды, находящейся в контакте с раствором через водопроницаемую мембрану. Найти константу диссоциации уксусной кислоты при 0 ºС. Можно ли определить константу диссоциации уксусной кислоты в воде при 0 ° С, используя другие коллигативные свойства? Ответ подтвердите оценками.
213. (5/2-06). При 30 ° С давление паров над водным раствором сахарозы равно 4159 Па. Давление пара над чистой водой при этой температуре равно 4241,7 Па. Найти осмотическое давление раствора.
214. (2/2-07)*. Для выделения чистой воды из морской вблизи берега моря вырыт колодец, стенки которого выполнены из материала, который можно рассматривать как идеальную селективную по воде мембрану, проницаемую для воды и не пропускающую растворенные в морской воде соли. Рассчитайте КПД такого способа. Мольную долю ионов в морской воде можно полагать равной 2 %.
Решение
215. (5/Э-07). Вы опять (см. зад. 237. (3/3-07)) находитесь на косе Тузла, разделяющей Черное (слева) и Азовское моря (справа). Справа от себя Вы видите косу Чушка, на которой группа террористов-сепаратистов стремительно закапывает Керченский пролив. Оцените возможные последствия этого смелого действия, если:
1) Керченский пролив – это единственный пролив, соединяющий два моря;
2) коса Чушка состоит из материала, способного служить селективной мембраной, проницаемой для воды;
3) высота косы над уровнем моря составляет 20 м;
4) содержание NaCl в морской воде составляет 18,5 г и 12,0 г на 1 л воды соответственно, а минерализация морской воды обеспечивается исключительно хлористым натрием.