15 января 2026
Российские и китайские ученые развивают низкотемпературное получение водорода из биомассы
24 декабря 2025
Ученые создают катализаторы эффективной переработки пищевых масел в экологичное авиатопливо

Краткая научная биография М.Г. Слинько
Юбилейные мероприятия в Москве и Новосибирске.
А.С. Носков. Два века математического моделирования
Воспоминания Р.А.Буянова, В.И. Быкова,В.А. Чумаченко
O.В. Крылову - 80 лет
Информация о конференциях
"Научные основы приготовления и технологии катализаторов" и
"Проблемы дезактивации катализаторов".
Профессор Г.Е. Заиков.50 лет в науке
Professor Jacques Fraissard
Доклад на проблемном семинаре, посвященном 90-летию М.Г. Слинько
Прошло два века математического моделирования в Институте катализа, учитывая, что это научное направление создавалось в середине 20-го века и продолжается сейчас - в 21-м веке. Сегодняшний доклад я хочу посвятить не столько перечислению всех тех результатов, которые достигнуты в математическом моделировании, сколько обозначению той роли, которую играет моделирование в развитии каталитических технологий и тех тенденций, которые, на мой взгляд, в этой области проявляются.

Постановление Пленума ЦК КПСС от 7 мая 1958 г. "Об ускорении развития химической промышленности и особенно производства синтетических материалов и изделий из них для удовлетворения потребностей населения и нужд народного хозяйства" послужило стартовым моментом в организации Института катализа. Затем, благодаря активным действиям Георгия Константиновича Борескова и Михаила Гавриловича Слинько, в Пост. ЦК КПСС и Совмина СССР от 23 июля 1958 г. было утверждено создание Института катализа в составе Сибирского отделения АН СССР в г. Новосибирске и там же дано задание построить в 1958-1959 г.г. лабораторный корпус Института катализа объемом 40 тыс. куб. м. и жилой дом площадью 6500 кв. м.
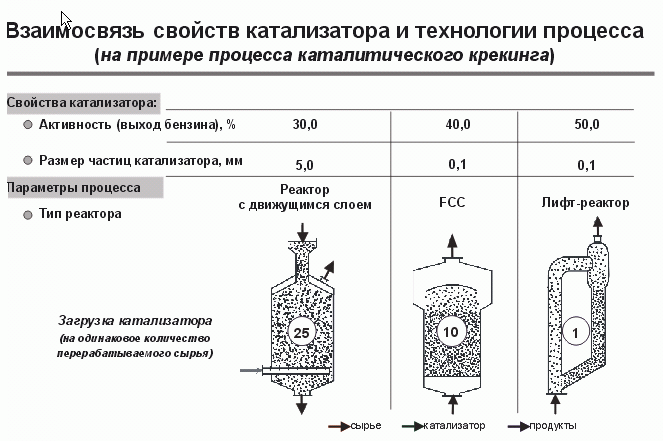
Лабораторный корпус был введен в эксплуатацию в 1963 г. На фотографии - митинг по случаю открытия этого корпуса. С первых дней в новом корпусе развернулись работы по математическому моделированию каталитических процессов. Специалисты в области катализа могут задать вопрос "если есть хороший катализатор, то что же может добавить математическое моделирование к его показателям?" Это можно показать на примере процесса крекинга. При увеличении активности катализатора всего в 1,5 раза в зависимости от того, как технологически оформлен процесс, габариты реактора могут уменьшиться в 25 раз и соответственно возрастет производительность катализатора. Это можно продемонстрировать на сравнении классического процесса с движущимся слоем катализатора, флюид-процесса и лифт-реактора (см. рис. 1). Хороший катализатор можно легко загубить плохим технологическим оформлением процесса. Математическое моделирование позволяет выбирать наилучшие технологические решения, максимально использующие все свойства катализатора.
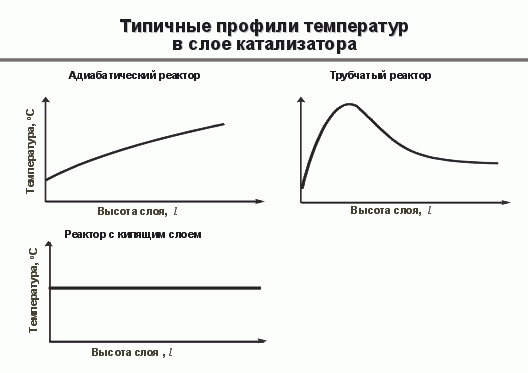
Если двигаться по классическому пути увеличения масштабов реактора на примере трубчатого реактора окисления этилена в окись этилена, то это такой маршрут: лабораторная установка - пилотные испытания - опытный реактор - промышленный реактор. Это достаточно длинный, продолжительный процесс. Естественно возникает желание ускорить это движение. Реально используются в промышленности несколько типов реакторов: с кипящим слоем катализатора, с движущимся слоем, с восходящим потоком катализатора, трубчатые и адиабатические с промежуточным нагреванием (охлаждением) реакционной смеси. Перед исследователем встает вопрос: как выбрать реактор для того или иного процесса? Одним из главных критериев является организация теплообмена. На рис. 2 приведены типичные профили температур для основных типов реакторов. Адиабатический реактор для экзотермического процесса всегда связан с повышением температуры, трубчатый реактор имеет температурную кривую с забросом, т.н. "горячую точку", реактор с кипящим слоем может обеспечить изотермический режим. При таком разнообразии всегда встает вопрос: какому типу отдать предпочтение? Одним из главных критериев является тепловыделение. Адиабатический многослойный реактор с промежуточным теплоотводом редко работает эффективно при адиабатических разогревах выше 150-200 ºС. Трубчатый реактор позволяет работать при разогревах 400-500 ºС, а реактор с кипящим слоем ограничений практически не имеет. Сейчас реализуется процесс, который позволяет удерживать в слое температуру около 350 º С при разогреве в три тысячи градусов. Для решения проблем о выборе оптимального реактора, его проектировании и строительстве и развивается методология математического моделирования.
Математическое моделирование - это интеграционная наука, которая включает в себя законы химии, физики, инженерной науки и методы анализа тех моделей, которые построены. В итоге мы выбираем модель для проектирования и управления каталитическим процессом. На рис. 3 конспективно представлены основные результаты по разработке метода математического моделирования, которые получены за прошедшие годы. Первая и основная база, с которой начинается движение - это разработка кинетических моделей, что несколько утеряно за последние годы. Оптимальная пористая структура зерна катализатора, влияние диффузионных ограничений, организация пористой структуры - следующий уровень вопросов. Далее следуют математические модели каталитических процессов в неподвижном слое, в кипящем слое и процессов с фазовыми превращениями. Оптимальное управление каталитическим процессом, в том числе при дезактивации катализатора, требует ответа на вопрос - как во времени менять температурные режимы. И, наконец, методы анализа построенных математических моделей. Здесь мы сталкиваемся с моделями с сосредоточенными параметрами - это обычные дифференциальные уравнения; с распределенными параметрами - это уравнения с частными производными.

Что может дать метод математического моделирования? Одной из первых работ, которая продемонстрировала возможности метода мат. моделирования, было открытие явления автоколебаний скорости реакции окисления водорода. Авторы экспериментальной части этой работы Владимир Беляев и Марина Слинько показали, что при изменении давления кислорода есть области, где наблюдались колебания скорости, и есть области, когда они исчезали. Объяснить это достаточно сложно, но удалось предложить такие кинетические модели, которые позволяют при анализе системы уравнений теоретически определить области, когда такие колебания существуют, и при каких параметрах исчезают. Совместные расчеты М.Г. Слинько и
Г. Чумакова показали возможности таких кинетических моделей.
Теперь коротко остановимся на различных моделях реакторов. Первый и самый простой и распространенный тип каталитического реактора - это реактор с неподвижным слоем катализатора. С чем мы сталкиваемся? Первый уровень - это химические превращения с тепло- и массопереносом внутри зерна катализатора. Второй - обмен зерна веществом и теплом с газовым потоком, третий - перенос тепла и вещества по слою катализатора, и наконец - теплопередача через наружную стенку реактора. Вот те факторы, которые определяют эффективность каталитического процесса в неподвижном слое. В связи с этим вырисовывается иерархический уровень, введенный М.Г. Слинько - это некая последовательность стадий, последовательность действий, которые необходимы для адекватного описания процесса. Первый естественный уровень - это кинетический, затем изучаем процесс внутри зерна - перенос вещества и тепла, далее - процесс в слое катализатора и перенос к наружной стенке. И верхний уровень- это модель реактора, где учитывается теплообменные поверхности; где также следует учитывать смешение и распределение газовых потоков. Каждая модель нижнего уровня входит в верхний со своими неизменными свойствами.
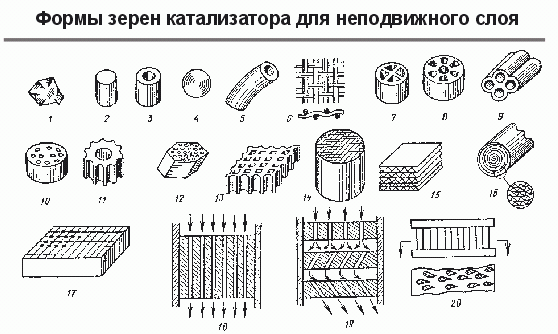
На рис. 4 показаны разные формы зерен катализаторов - это лишь часть того многообразия форм, которые существуют. Должны существовать методы выбора оптимальной формы зерна катализатора. Моделирование процесса на зерне катализатора всегда составляло существенную часть работ, проводимых в Институте катализа. Хотя в начале 60-х годов XX века, когда посылались работы по математическому моделированию на зерне катализатора в научные журналы, сотрудники порой получали ответы, что "мы не публикуем статьи, связанные с переработкой сельскохозяйственного зерна", хотя это были журналы химического профиля.
Если попытаться описать относительно простые процессы, которые происходят в неподвижном слое, то появляется двухфазная модель, жаргонное название которой D2, которая учитывает большинство упомянутых выше факторов. Эта модель широко применяется для описания большинства каталитических процессов.
Возникает вопрос - а что может дать такая простая модель? Что она позволяет делать? Прежде всего описать процесс окисления SO2 в SO3 для обратимой реакции. Как можно заметить, для того, чтобы приблизиться к равновесной степени превращения, необходимо вести процесс в нескольких слоях катализатора. При росте превращения SO2 температура в слое возрастает и в итоге процесс упирается в равновесие. Далее следует охладить газ, провести процесс во втором слое, снова охладить газ и таким образом построить огибающую равновесные степени превращения. Возникает вопрос - какое количество катализатора должно быть в разных слоях, чтобы при наименьших количествах катализатора в слоях обеспечить наилучшее приближение к равновесию. Такую задачу позволяет легко решать математическое моделирование. Во-первых - это как наилучшим образом распределить катализатор между слоями, во-вторых - до каких температур при этом охлаждать газ. Это сложные двухпараметрические задачи - выбор оптимальных количеств катализатора и входных температур. Созданные модели позволяют строить большие и сложные аппараты, диаметром в несколько метров (до 10 метров). Из этой же модели были получены оценки параметров тепловых фронтов в слое катализатора. Эти результаты были получены О.В. Киселевым ( рис.5). Как оказалось, из этих теоретических результатов мы можем получить достаточно много технологических рекомендаций.

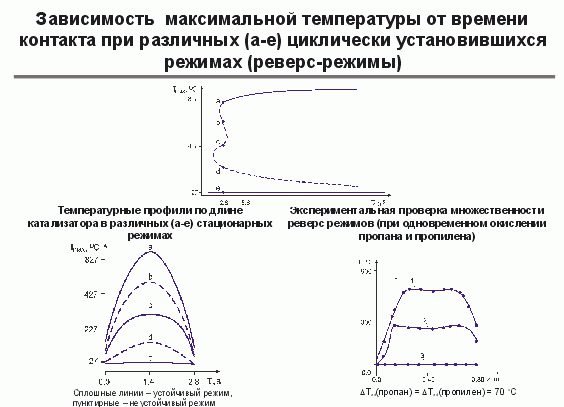
Из уравнения видно, как зависит скорость движения теплового фронта, значение максимальной температуры от теплопроводности слоя катализатора; как они зависят от коэффициента массообмена, а коэффициент массообмена - это размер зерен катализаторов, т.е. мы знаем, как управляя размером зерен катализатора, влиять на температуру, на скорость движения фронта. Т.е. из теоретических зависимостей мы выходим непосредственно на технологические рекомендации. В этом значимость и роль математических моделей для каталитических процессов. И как всегда, возникают интересные моменты, - например, когда из анализа построенной модели получаешь некоторые необычные результаты, которые находят затем прямое экспериментальное подтверждение. Это результаты, полученные на основе двухфазных моделей для процессов с периодическим реверсом газового потока. Такие схемы в обиходе называются "качалкой". Из теоретических результатов следует, если две реакции с разными кинетическими параметрами одновременно протекают в слое катализатора, то возможны 5 устойчивых циклических режимов. На кривой "время контакта-максимальная температура" видно (рис. 6), что существуют 5 циклических режимов. Температурные профили по длине показаны на рисунке. Непрерывные линии - это устойчивые режимы, штриховые (полученые численно) - это неустойчивые режимы. Сначала это было получено теоретически, а спустя 3-4 года ученые Штутгарского университета под руководством профессора Айгенбергера для совместного окисления пропана и пропилена экспериментально получили 3 устойчивых режима. Эти данные были использованы для строительства серии установок типа "качалки". Такая установка была построена, например, на Бийском олеумном заводе. Как известно, процесс технологически состоялся, когда построена не первая установка (первых строят много - они и остаются единственными и неповторимыми), а вторая установка. Это значит, что первая установка понравилась и принимается решение о строительстве второй. На Бийском олеумном заводе первая установка построена в 1990 г., десять лет она проработала, затем завод построил вторую, т.к. такой процесс устраивает завод по своим технологическим показателям.
Гораздо сложнее выглядят трубчатые аппараты. В таблице 1 приведены данные по некоторым видам реакторов. Обращаю ваше внимание на количество трубок в таких аппаратах - от скромных 5 тысяч до 20 тысяч трубок . Длина трубок по 6-8 метров. Такие аппараты достаточно капризны. Как вы помните, температурные кривые имеют "горячую" точку. На температуру "горячей" точки влияет в первую очередь температура теплоносителя. Увеличение температуры теплоносителя на 2 ºС может вызывать рост температуры катализатора на 20 ºС и более. Нужно очень аккуратно выбирать диаметр трубки, чтобы не получить взрывные процессы. При быстром разогреве возможно спекание катализатора, то что в технологической практике называют "козлом". Представьте, как опытный технолог наставляет молодого перед пуском нового аппарата: "веди процесс осторожно, а за "козла" ответишь!".
Таблица 1
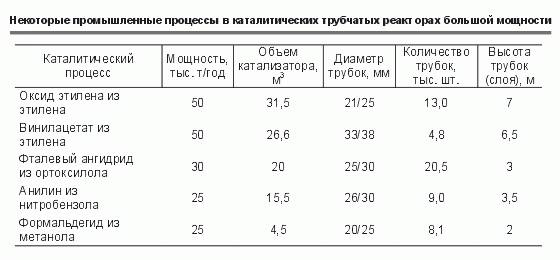
Вы видели, какие габариты имеют трубчатые реактора с трубками длиной до 6 м, поэтому естественно появляется желание уменьшить габариты реактора. Одна из разработок метода мат. моделирования - это создание т.н. комбинированных реакторов - трубчатых аппаратов с адиабатической приставкой. Часть превращения реагентов идет в трубках с большим разогревом, когда надо снять большое количества тепла, а часть - в адиабатической приставке. Что это дает? Здесь показаны (рис. 7) данные для окисления метанола в формальдегид. Есть 2 варианта. Либо вы ведете процесс в трубке при времени контакта 0,6 сек. Либо вы сначала ведете процесс в трубке при времени контакта 0,3 сек., а затем - в адиабатической приставке. Это дает сокращение количества катализатора на 25 % и, соответственно, уменьшаются габариты реактора.
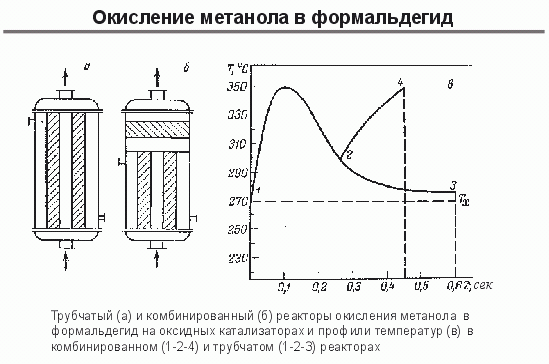
Какова роль селективности катализатора в трубчатых реакторах? В реакторе окисления этилена в окись этилена диаметр трубок около 20 мм, и несмотря на разные ухищрения - переход от шариков к кольцам- не удается увеличить диаметр трубок и, соответственно, количество трубок велико. Если же селективность по окиси этилена удастся увеличить на 10-15 %, это позволит увеличить диаметр трубок с 21 до 27 мм, а это значит, можно сократить количество трубок в 2 раза. Вот так сказываются свойства катализатора. За счет повышения его селективности по окиси этилена снижается количество продуктов полного окисления, уменьшается разогрев, что позволяет увеличить диаметр трубок.
Рассмотрим теперь насколько капризны трубчатые аппараты и как надо выбирать температуру теплоносителя, чтобы снять избыточное тепло для процесса окисления орто-ксилола во фталевый ангидрид. Повышение температуры на 3 ºС приводит фактически к срыву процесса и переходу в высокотемпературную область. Небольшие колебания, крайне высокая чувствительность процесса, и аппарат выходит на перегрев, что вызывает выход из строя катализатора. Надо выбирать таким образом диаметр трубок, чтобы была не очень высокая параметрическая чувствительность. В реальных условиях температура всегда колеблется и один из главных показателей трубчатых аппаратов - не очень высокая чувствительность к входной температуре, к температуре теплоносителя.
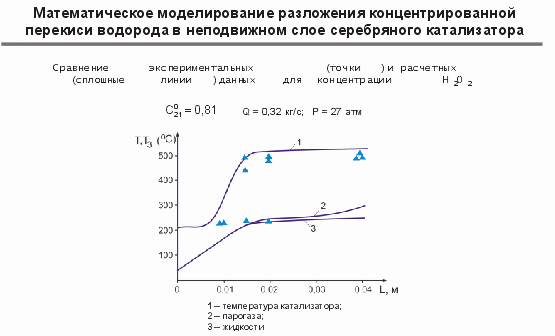
Следующий достаточно сложный процесс - это процесс с фазовыми превращениями. Здесь иерархический уровень такой же, как в неподвижном слое, но надо учитывать наличие в зерне катализатора одновременно смоченной поверхности и несмоченной. Так в процессе разложения перекиси водорода часть поверхности катализатора будет контактировать только с жидкой фазой, а часть - с газовой фазой. Приходится рассматривать две модели и учитывать взаимный переход жидкой фазы в газовую. Метод мат. моделирования позволяет прогнозировать температуру в слое катализатора (Т1), температуру парогазовой смеси (Т2) и жидкой фазы (Т3). На рис. 8 вы видите и данные расчета, и данные эксперимента.
Следующая серия работ по распространенности и по объему - это процессы в кипящем слое катализатора. На сегодня самый крупнотоннажный процесс в кипящем слое - это синтез акрилонитрила. Аппараты огромные - диаметром около 10 м, общей высотой 20 м. Возникает вопрос - как перейти от данных для аппарата с диаметром 1 см к аппарату диаметром 10 м? Кипящий слой особенно капризен с точки зрения масштабного перехода. Что происходит в кипящем слое? По мере движения газа снизу вверх происходит увеличение пузыря газовой фазы за счет присоединения к нему более мелких пузырей. И порой, на выходе из аппарата диаметр газового пузыря (а внутри него нет катализатора и не происходит превращение реагентов), может достигать нескольких метров. Для глубокого превращения реагентов приходится идти на значительное увеличение количества катализатора или разрабатывать различные способы борьбы с такими пузырями. Для этого существуют разные возможности. Например, существуют такие режимы, когда газовые пузыри становятся неустойчивыми, они образуются и в тоже время при определенных условиях разрушаются. Об этом я скажу чуть позже.
Я хочу показать, как связан масштаб реактора с изменением коэффициентов массообмена. В кипящем слое активность катализатора всегда высока и все лимитируется подводом реагирующего вещества к поверхности катализатора. Активность катализатора можно увеличить в 10 раз, но аппарат этого не почувствует. Следовательно все определяет коэффициент массообмена, а это - габариты реактора, эффективность процесса, выход продукта. Для свободно кипящего слоя с увеличением диаметра аппарата уменьшается коэффициент массообмена (см. рис. 9). Это означает, что при увеличении диаметра аппарата для той же производительности количество катализатора надо увеличить в 2 раза. Чтобы решить эту проблему и переходить от одного размера на следующий без резкого увеличения удельной загрузки катализатора, было предложено такое направление, как организованный кипящий слой. Для организованного кипящего слоя диаметр аппарата увеличивается, а коэффициент массообмена остается прежним. Это достигалось разработкой т.н. малообъемных насадок. Существуют разные виды насадок. Когда аппарат с кипящим слоем наполняется такими насадками, это приводит к разрушению газовых пузырей, пузыри не достигают больших размеров, и переход от одного диаметра реактора к другому не требует резкого увеличения удельного количества загружаемого катализатора.
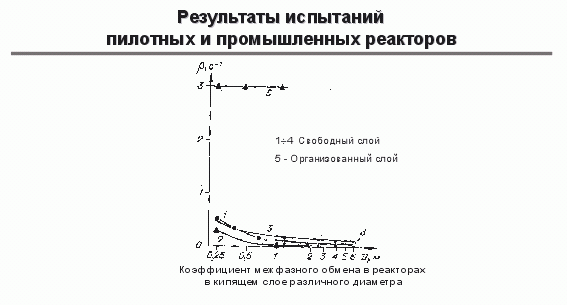
Многие процессы идут эффективно в неподвижном слое. Когда возникает желание сократить размеры аппарата, то можно перейти к кипящему слою. Если взять свободно кипящий слой, то эффективно можно осуществить только синтез винилацетата с такой же эффективностью, как в неподвижном слое. Если перейти к организованному кипящему слою, то большое количество различных процессов становится более эффективными, чем в неподвижном слое. Но остается часть процессов, которых не удается реализовать в кипящем слое - требуются слишком большие коэффициенты массообмена, которые не удается обеспечить.
Второе направление борьбы за эффективность кипящего слоя - это т.н. переход к турбулентному кипящему слою, когда газовые пузыри становятся гидродинамически неустойчивыми. Свойства этого слоя - газовые пузыри имеют только малый размер; скорости межфазного обмена весьма высоки.
Развитие математического моделирования привело к созданию большого количества промышленных процессов. В таблице 2 представлена только небольшая часть. Это - окисление метанола в формальдегид в аппаратах с адиабатическими слоями и в трубчатых аппаратах с приставками, большой объем работ был связан с переходом на новые катализаторы в производстве серной кислоты, процессы парциального окисления - это окисление этилена в окись этилена, окисление нафталина во фталевый ангидрид, большое количество установок специального назначения (регенерация газов для ракетно-космической техники); большое количество установок на основе реверс-процессов, создание которых было бы невозможно без методов математического моделирования.
Таблица 2

|
N |
Процесс |
Год |
Место реализации |
|
1 |
Окисление метанола в формальдегид в трубчатом реакторе с адиабатической приставкой |
1965 |
Новосибирский |
|
2 |
Окисление метанола в формальдегид в реакторе с адиабатическими слоями катализатора | 1980 | Кемеровское ПО "Карболит" ("ОАО "Токем"). |
| 3 | Окисление диоксида серы в триоксид | 1960-1992 | Проведена модернизация и введено в эксплуатацию более 15 установок по получению серной кислоты на различных заводах. |
| 4 | Окисление нафталина во фталевый ангидрид | 1965-1975 | Челябинский химический завод; Авдеевский химический завод; Рубежанский химический комбинат. |
|
5 |
Окисление этилена в окись этилена в |
1970-1975 |
ОАО "Салаватнефтеоргсинтез"; |
|
6 |
Дегидрирование |
1974 |
Завод СК, г. Тольятти. |
|
7 |
Синтез винилхлорида в неподвижном слое катализатора |
1969 |
Новомосковское ПО "Азот" |
|
8 |
Синтез винилацетата в неподвижном слое катализатора |
1970 |
Северодонецкое ПО "Азот" |
|
9 |
Тримеризация хлорциана в цианурхлорид на активированном угле |
1970 |
ПО "Оргстекло" |
|
10 |
Окислительный |
1970-1985 |
Саратовское ПО |
|
11 |
Очистка газов от оксидов азота |
1988, 2000 |
Федеральное |
|
12 |
Адсорбционно-каталитическая очистка газов от органических соединений |
1998 |
ОАО "Западносибир-ский металлургический комбинат" |
|
13 |
Устройства генерации газа для систем ракетно-космической техники |
1963-1992 |
Разработано около |
|
14 |
Очистка газов в режиме Реверс-процесса: |
1978-2000 |
Более 50 установок в РФ, США, Австралии и др. странах |
Я считаю одними из наиболее перспективных направлений развития технологии каталитических процессов и моделирования, пожалуй, два направления: появление новых физических методов исследования технологических процессов, например, рентгеновской томографии и второе - внедрение в технологию каталитических процессов методов вычислительной гидродинамики. Благодаря развитию вычислительной техники и математического моделирования можно считать и решать очень сложные процессы тепло- и массообмена на основе прямого решения уравнения Новье-Стокса.
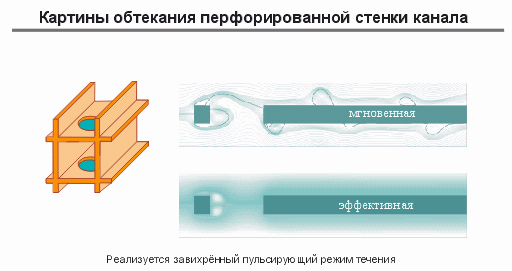
На ближайшие годы эти два направления будут в значительной мере определять развитие технологий каталитических процессов. На рис.10 показано, каким образом происходят газовые течения в сотовых катализаторах при наличии отверстий и показаны методы интенсификации массообмена для сотовых катализаторов. Современная вычислительная гидродинамика позволяет считать процессы с химическими реакциями.
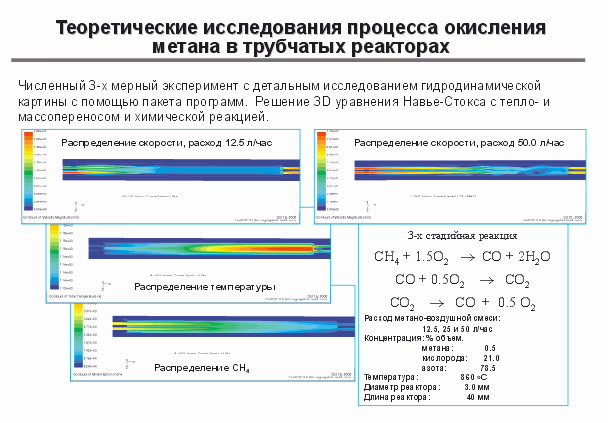
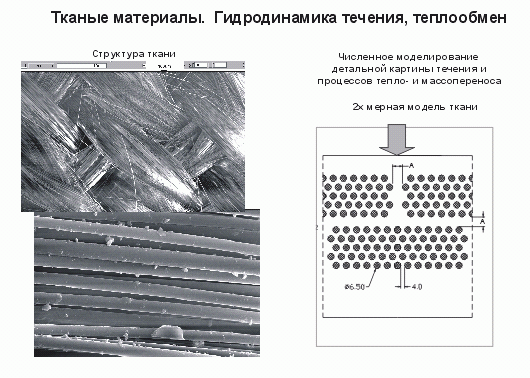
Например, на рис. 11 показаны расчеты процесса горения метана в керамических трубочках. Видно, как в зависимости от скорости течения меняется режим, можно видеть распределение температур в трубке, превращение метана по длине трубки. Все эти расчеты выполнены на основе простейшей трехстадийной схемы окисления метана через образование СО. Можно считать процессы массообмена для систем с катализаторами на основе стеклоткани. На рис. 12 показана реальная стеклоткань (микрофотография) и приведены расчеты фильтрации газового потока через такую систему. Это удается расчитать на основе трехмерной модели Новье-Стокса. Результат немного необычный. Газовый поток будет фильтроваться не на всех местах. Небольшая часть потока может пройти через мелкие волокна, а большая часть газового потока будет фильтроваться между нитями. Массообмен будет сосредоточен на входных участках в значительной степени и на выходных - в меньшей степени. Возникает проблема оптимизации геометрической структуры для стеклоткани.

Большой интерес, на мой взгляд, может представлять то, что сейчас удается рассчитать процессы на суспендированном катализаторе для жидкофазного процесса с мешалкой. Для одинаковых стартовых условий будут устанавливаться различные режимы в зависимости от плотности катализатора при одинаковых режимах работы мешалки. В таких условиях будет наблюдаться другой выход продуктов реакции даже, если активность катализаторов будут одинаковой. Это может найти применение для процессов жидкофазного окисления, жидкофазного гидрирования, и может быть, для самого интересного направления - процессов полимеризации на суспендированных катализаторах - для разработки нового поколения реакторов.
Ранее я говорил о применении методов рентгеновской томографии. Это, например, исследование процессов гидрирования в неподвижном слое, которые развиваются И.В. Коптюгом и В.А. Кирилловым. Метод позволяет наблюдать процесс заполнения слоя жидкой фазой и как меняется заполнение при изменении скорости подачи. Уникальные возможности метода позволяют наблюдать динамику заполнения слоя в зависимости от условий. При росте температуры жидкая фаза исчезает, потом снова идет заполнение слоя жидкой фазой, струя растекается и весь аппарат снова заполняется жидкой фазой. Такие процессы могут носить циклический характер.
Методы математического моделирования и развитие технологий каталитических процессов были предметом постоянных конференций ХИМРЕАКТОР. В таблице 3 приведен перечень этих конференций, которые проходили, начиная с 1963 г., и кончая последней, которая прошла в Казани и Берлине в 2003 г. Следующую конференцию в 2006 г. нам предложили провести на о. Мальта в Средиземном море. Первая конференция 1963 г. имела скромное название "Всесоюзное совещание по моделированию и оптимизации каталитических процессов".
Таблица 3
Конференции " Химреактор"
|
N |
Место проведения |
Год |
|
N |
Место проведения |
Год |
|
1 |
Новосибирск |
1963 |
|
9 |
Гродно |
1986 |
|
2 |
Новосибирск |
1965 |
|
10 |
Тольятти |
1989 |
|
3 |
Киев |
1968 |
|
11 |
Алушта |
1991 |
|
4 |
Новосибирск |
1971 |
|
12 |
Ярославль |
1994 |
|
5 |
Уфа |
1974 |
|
13 |
Новосибирск |
1996 |
|
6 |
Дзержинск |
1977 |
|
14 |
Томск |
1998 |
|
7 |
Баку |
1980 |
|
15 |
Хельсинки |
2001 |
|
8 |
Чимкент |
1983 |
|
16 |
Казань - Берлин |
2003 |

Так выглядел 1-й юбилей (50 лет) Михаила Гавриловича в 1964 г. 40 лет пролетели очень быстро.

В заключении я хотел выразить благодарность всем тем людям, которые вместе с Михаилом Гавриловичем развивали в нашем Институте методы математического моделирования каталитических процессов.
А.С. Носков
д.т.н., профессор
Институт катализа Со РАН